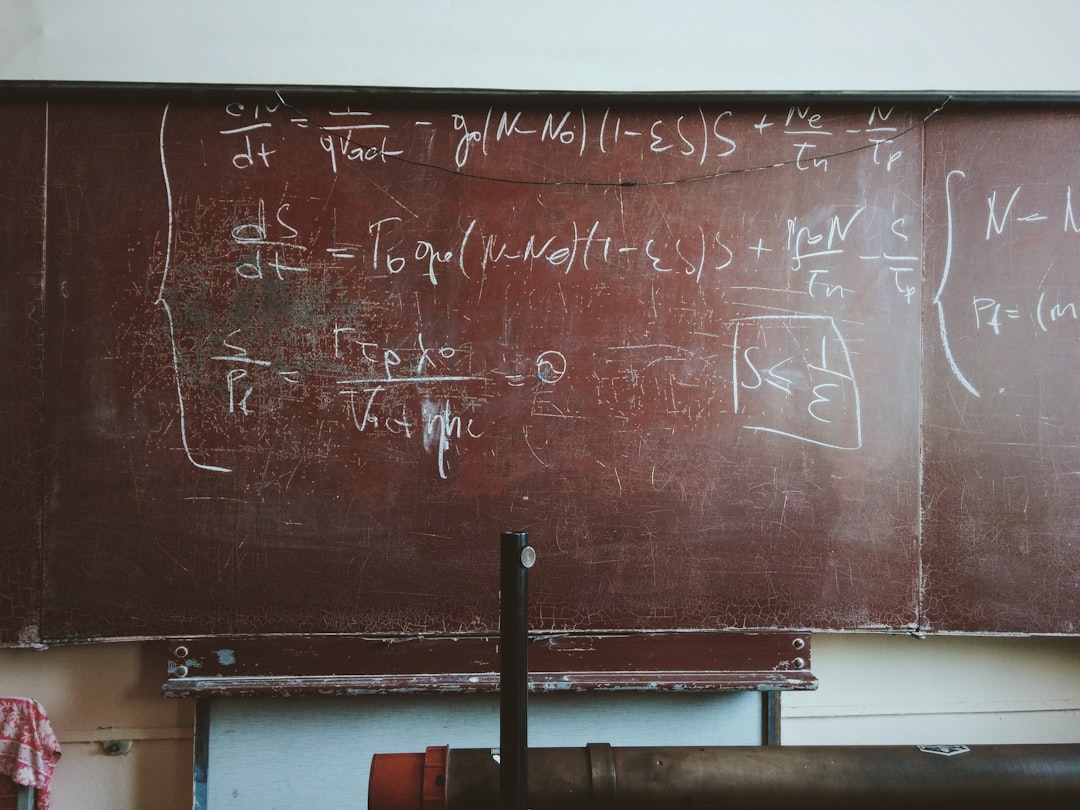Insights into the non-Markovian way stochastic processes traverse heteroclinic networks

What is it about?

Heteroclinic networks can be visualised as directed graphs (nodes with arrows connecting them). In the presence of noise, how stochastic processes traverse the network may depend on their history, that is, the sequence of nodes visited may be non-Markovian. We consider the behaviour of a process near a saddle equilibrium under different initial conditions and use this to determine the order of the non-Markovian process and the corresponding transition probabilities.

Featured Image

Photo by WrongTog on Unsplash

Photo by WrongTog on Unsplash

Why is it important?

This work is important for several reasons: Firstly, heteroclinic networks have been used to model cognitive phenomena. However, the non-Markovian properties of heteroclinic networks (which correspond to necessary properties of many cognitive processes) have not been utilized. This work will enable future development in this type of application, and perhaps others. Secondly, we expand on previous work where a local map of a noisy saddle was made by considering the application of that map to different initial conditions (in particular the case when the initial condition is not centred on the heteroclinic network). This may be of use to many applications in stochastic differential equations where processes may pass near saddle equilibria of the underlying systems. Thirdly, we show that our new results do converge to the deterministic solutions as the noise becomes small, but that this convergence tends to be quite slow and, consequently, non-Markovian behaviour may be observed even when the noise amplitude is (what we consider to be) small. This is useful to keep in mind for anyone simulating heteroclinic networks who may have assumed that, due to their choice of eigenvalues, the dynamics would be strictly Markovian.

Perspectives